Points And Boxes
Starting problem
The starting problem is given a line and labeled points on that line we define a binary string by taking a line segment that covers some points. Covered points are a one and non-covered points are a zero. For example given points \(\{1,2,3\}\) on the line if a line segment covers points \(\{1,3\}\), then it has a binary string \(101\).
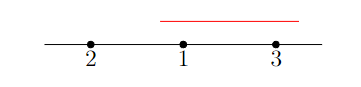
We define a binary set as the set of all binary strings for a given set of points. For building a binary set you are allowed to change the length of the line segment between binary strings, but not rearrange the points.
Question 1. What are the maximum number of points where you can get a binary set?
Starting problem solution
The answer is two. We can solve two points directly, but when we move to three points the middle point blocks just the two outer points from being covered by a line segment. That is if we labeled our points from left to right as \(\{1,2,3\}\), then we can’t get the binary string \(101\).
Two dimensions
In two dimensions we now place points on a plane and instead of covering with a line segment we cover with a rectangle. For a given covering to work we can change the length and width of the rectangle, but we cannot rotate it. Also, the points can be chosen anywhere on the plane, but must be in the same place for the entire binary set.
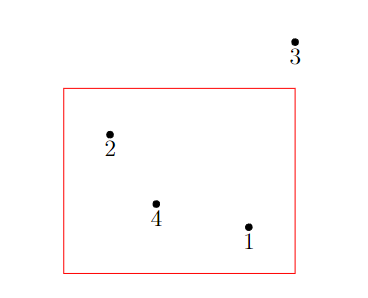
Solution in two dimensions
The answer is four. We can solve this by placing the points in a square, then moving one point up a little, one point slightly to the left, one point slightly to the right, and the final point slightly down. You can also think of this as rotating the square by a small (under 45 degree) amount.

From there we can easily make every covering combination. Below are several ways to show why five points can’t be solved.
Solution 1: Projections
Lemma 2. If two or more points share either the same \(x\) or \(y\) component, then a binary set for five points does not exist.
Proof. Let the five points be labeled \(p_1\), \(p_2\), \(p_3\), \(p_4\), \(p_5\) where \(p_i = (x_i, y_i)\), then without loss of generality assume that points \(p_1\) and \(p_2\) share the same \(x\) component, \(x_1 = x_2\), and \(y_1 < y_2\). If there exists a point \(p_j\) where either \(y_j \leq y_1\) or \(y_j \geq y_2\), then we can’t form rectangles for \(\{p_1, p_j\}\) and \(\{p_2, p_j\}\) since one of the two rectangle must contain all three points. Thus points \(p_3\), \(p_4\), and \(p_5\) must have \(y\) components between \(p_1\) and \(p_2\). Order \(p_3, p_4, p_5\) by their \(x\) components, that is make \(x_3 \leq x_4 \leq x_5\), then two of the points must either be greater than or equal to \(x_1\) or less than or equal to \(x_1\) without loss of generality assume less than (for greater than use \(p_5\) instead of \(p_3\)). This makes it impossible to get both \(\{p_1, p_3\}\) and \(\{p_2, p_3\}\) since one of those rectangles must contain \(p_4\). Therefore for a solution of five points to be possible all \(x\) and \(y\) components must be distinct. ◻
Lemma 3. When working in one dimension with \(n\) points you can cover at most \(n-1\) pairs of points.
Proof. This follows from the fact that in one dimension you can only cover a pair of points if there is no point in between them. ◻
Theorem 4. There exists no binary set to cover five points in two dimensions.
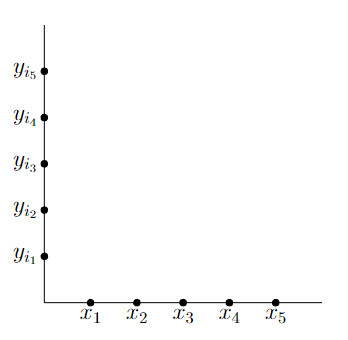
Proof. Let the five points be labeled \(p_1\), \(p_2\), \(p_3\), \(p_4\), \(p_5\) where \(p_i = (x_i, y_i)\), then from Lemma 2 we can strictly order the \(x\) component, that is \(x_1 < x_2 < x_3 < x_4 < x_5\). This immediately allows us to box the pairs \(\{p_1, p_2\}\), \(\{p_2, p_3\}\), \(\{p_3, p_4\}\), and \(\{p_4, p_5\}\). Now there are 6 remaining pairs of 2 points we need to box. However we can only manipulate the \(y\) component of the five points, see figure 4. Thus by Lemma 3 we can get, at most, 4 more pairs. Therefore we will be unable to cover the last two pairs of points. ◻
Solution 2: Partitioning the plane
Let \(p_1, p_2\) be points, then define \(R(p_1,p_2)\) as the rectangle made from \(p_1\) and \(p_2\) as corners. This rectangle, \(R(p_1, p_2)\), will be called the minimal rectangle of \(p_1\) and \(p_2\).
Given this minimal rectangle we can partition the plane into \(8\) octants by extending the \(4\) lines in either direction. We will label the octant where both the \(x\) and \(y\) components are greater than that of either \(p_1\) or \(p_2\) as \(0\)th octant then increment counterclockwise around.
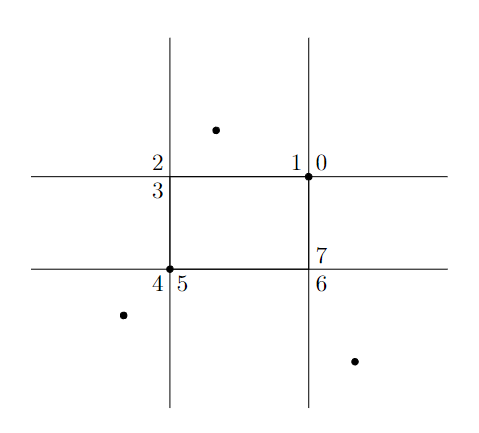
Lemma 5. If points lies in any of the octant combinations \(03\), \(04\), \(26\), \(27\), \(47\), \(40\), \(62\), \(63\) for a given minimal rectangle, then we can’t rectangle all the pairs.
Proof. If points are in those octants then making a rectangle cover those points requires boxing one of the partitioning points. ◻
Theorem 6. There exists no binary set to cover five points in two dimensions.
Proof. Let the five points be labeled \(p_1\), \(p_2\), \(p_3\), \(p_4\), \(p_5\) where \(p_i = (x_i, y_i)\), then from Lemma 2 we can strictly order the \(x\) component, that is \(x_1 < x_2 < x_3 < x_4 < x_5\). Now consider \(R(p_2,p_3)\), \(R(p_2,p_4)\), \(R(p_3,p_4)\) from Lemma 5 \(p_1\) and \(p_5\) must lie in octants 3 and 7 or in octants 1 and 5 for each rectangle. Without loss of generality we will assume 3 and 7 (if using 1 and 5, then switch \(y\) components with \(x\) components). This forces \(y_1\) and \(y_5\) to be between \(y_2\), \(y_3\), and \(y_4\). In particular two points from \(y_2\), \(y_3\), \(y_4\) must either be greater than or less than \(y_1\) and \(y_5\). Without loss of generality we will assume greater and we can label those \(y_3\) and \(y_4\). This gives the following inequalities
\[\begin{aligned} &x_1 < x_2 < x_3 < x_4 < x_5 \\ &y_2 < y_1 < y_3 \\ &y_2 < y_1 < y_4 \\ &y_2 < y_5 < y_3 \\ &y_2 < y_5 < y_4 \\ \end{aligned}\]By Lemma 2 \(y_3 \not = y_4\), so we have two options. If \(y_4 > y_3\), then we can’t make the pair \(\{p_2, p_4\}\) without \(p_3\) being included. If \(y_4 < y_3\), then we can’t make the pair \(\{p_3, p_5\}\) without \(p_4\) being included. Thus there exists no binary set to cover five points in two dimensions. ◻
Solution 3: Perturbations of minimal rectangle containing all points
This solution was given by a fellow grad student, Jared Brannan, who was the person who posed the problem to me.
Define \(R(P)\) as the minimal rectangle containing all the points, \(P = \{p_1, p_2, \dots, p_n\}\).
Lemma 7. For any set of points \(P\), the minimal rectangle \(R(P)\) will contain at least one point on each edge (corner counts as both edges).
Proof. This follows immediately from the definition of minimal rectangle containing all the points, since if an edge did not contain a point we could reduce the size of the rectangle. ◻
Theorem 8. There exists no binary set to cover five points in two dimensions.
Proof. Let \(P = \{p_1, p_2, p_3, p_4, p_5\}\), then by Lemma 7 \(R(P)\) either has two points sharing an edge or at least one fully interior point. If two points share an edge, then by Lemma 2 we can’t get all binary sequences for five points. If we have a fully interior point, then we can’t cover just the exterior points. Thus there exists no binary set to cover five points in two dimensions. ◻
Higher dimensions
The final question is what is the formula for an \(n\) dimensional space? The same restrictions apply; points can be placed anywhere but must remain constant for a full binary set, you are covering with \(n\) dimensional hyperrectangles where any side can be changed in length, but they cannot be rotated.
Solution in higher dimensions
The answer for \(n\) dimensional space is \(2n\). Solutions 1 and 3 from two dimensions generalize pretty well, but solution 3 is the easiest to give. So I will give a proof outline for solution 1 and a full proof of solution 3.
For solution 1, first show the lower bound. We can proceed by induction. Strictly order one of the dimensions use this to give a certain set of combinations, then using the remaining \(n-1\) dimensions to solve the remaining combinations. The upper bound is exactly the same argument, but we can show their are more combinations then we can solve.
Now for the full proof using the ideas from solution 3.
Theorem 9. There exists a binary set to cover \(2n\) points in \(n\) dimensions.
Proof. Construct a \(n\) dimensional hypercube around the origin. This cube has \(2n\) faces, so place a point at the midpoint of each face. Now to get a given combination of points covered, we take the hypercube and move every face corresponding to a point we don’t want covered towards the origin. Since we can do this for any combination of points we get the full binary set. ◻
Theorem 10. There exists no binary set to cover \(2n + 1\) points in \(n\) dimensions.
Proof. Let \(P\) be the set of \(2n + 1\) points and construct the minimal hyperrectangle \(R(P)\) for the points \(P\). Now we have two cases either two points lie on the same face (that is they share some coordinate) or their is a fully interior point. If there is a fully interior point, then we can’t get all binary string containing \(n-1\) one values. If there are two points sharing the same component, then we can make the same argument as in Lemma 2 to show that we can’t get all binary pairs. Thus there exists no binary set to cover \(2n+1\) points in \(n\) dimensions. ◻
Where this problem came from
This problem was posed as a fun problem with no applications. It came from Jared, who gave solution 3, when looking at Shattered sets.
Open questions and further generalizations
-
For another solution of the 2d case I was hoping to use graph theory to make a planarity argument. That is, compare trying to box 5 points on the plane to the complete \(K_5\) graph being non-planar. I wasn’t able to come up with a nice mapping between the two. So the open question is does there exist a consistent mapping between the \(K_5\) graph and boxing points such that \(K_5\) being non-planar proves that we can’t box 5 points? This may generalize well using hyper graphs or some genus argument on the space.
-
How does this problem change if we allow for rotation? My conjecture is that it is equivalent to adding one extra dimension.
-
How does this problem change if instead of rectangles we allow for different convex shapes? For example if using discs instead of rectangles you can show that four points is not possible in two dimensions.
-
Finally, what can be said if we instead allow for arbitrary sets of functions instead of shapes. For example the set of paths with restrictions on their curvature.